中学受験の理科ではつまずきやすい単元がいくつかあります。タイトルにある「電流」「浮力」「水溶液」はその中でも代表的な例です。この記事では中学受験の理科で苦手意識を覚えやすい単元をピックアップしつつ、理科の勉強法を紹介していきます。
中学受験を目指す子供たちが苦手な理科の単元って

中学受験を目指す子供たちが苦手になりやすい単元について紹介します。
算数的な思考を要求される単元
中学受験を目指す子供たちが、苦労する理科の単元はどこなのでしょうか。
まず、算数的な思考を要求される単元は苦手な子供が多いです。具体的には電流・浮力・てこ・滑車・水溶液などです。
理科の多くの単元は算数以上に覚えなければならない知識が多く、その上で計算を求められるため、解き方がわからなくなってしまう子供がたくさんいます。物理分野が主ですが、化学分野が苦手な子供も少なくありません。
苦手な単元を受験前まで残さないためにはどうすればよいか
理解しづらい単元に出会ったらその日のうちに復習し、それでも理解できない部分は塾や家庭教師の先生に質問しましょう。塾の場合、週テストがある塾ならばそれまでに理解し、さらに週テストの結果を受けて復習するという流れになります。家庭教師の場合、テストはないでしょうから、宿題や復習を通して週単位で実力を定着化させましょう。わからなかった部分は翌週にやり直して仕上げる流れです。
しかし、「こういうルーティンでいこう」と決めてもなかなか思いどおりには進まないもの。たいていの子供は、中途半端な理解のまま先に進んでしまいます。授業もどんどん進んでいきますから、今やっている内容についていくのがやっとなのです。
塾に通っている場合は、一か月に一度ぐらいの頻度でテストがあるはずですから、再度そこで復習のタイミングはあります。なんとかそこまでに仕上げられるようにしたいところです。家庭教師の場合も、先生と一か月ごとにわからなかった単元のチェックをしていくとよいでしょう。
単元別に見ていこう。具体的な勉強の進め方

苦手な子供の多い単元別に勉強の仕方を紹介します。
計算方法がわからない。電流の勉強の仕方
電流関連の単元では、基本的な知識をしっかり覚えこまなければなりません。とりわけ回路図の問題では、知識があやふやなまま計算をして、間違えるパターンをよく見ます。
まずは直列つなぎと並列つなぎの違いを覚えましょう。
直列つなぎ
直列つなぎでは、ふたつの電熱線を縦一列につなぎます。それぞれの電熱線を流れる電流は同じです。
並列つなぎ
並列つなぎでは、ふたつの電熱線を横に並べてつなげます。それぞれの電熱線にかかる電圧は同じです。
直列つなぎと並列つなぎにおける電熱線の発熱量
並列つなぎの場合、ふたつの電熱線にかかる電圧は同じです。そのため、太い電熱線のほうが大きな電流が流れて熱くなります。
直列つなぎではふたつの電熱線に流れる電流は同じです。そのため、電圧が大きくなる細い電熱線のほうが熱くなります。
それでは、同じ太さの電熱線の場合はどうなのでしょうか。長い電熱線ほど抵抗が大きくなり電流は流れづらくなります。
そのため、並列つなぎでは短い電熱線の発熱量が多いですし、直列つなぎの場合長い電熱線のほうが発熱量は多くなります。
| つなぎ方 | 特徴 | 発熱量 | |
|---|---|---|---|
| 直列つなぎ | 縦一列につなげる | 電流は同じ | 短い電熱線の発熱量が多い |
| 並列つなぎ | 横に並べてつなげる | 電圧は同じ | 長い電熱線の発熱量が多い |
電流は水の流れで考えてみよう
電流は水の流れに見立てて考えるとわかりやすいです。電圧の大きさは高いところから水を流すか、低いところから水を流すかの違いを想像して理解するとよいでしょう。高いところから流せば一秒間に流れる水の量は多くなります。つまり電圧が大きければ電流も多くなる仕組みです。
抵抗は水路に設けられた水車だと考えましょう。水車が大きいと水の流れを妨害してしまいますが、小さければそんなに邪魔にはなりません。抵抗も同じで、大きければ電流を少なくしてしまいますが、小さければ電流は多くなります。
浮力はどういうものかを理解して解こう
浮力も苦手な子供が多い単元です。浮力とはなにかを理解すれば解きやすくなります。
浮力ってなに?
水に物体を沈めようとして、浮いてきてしまった経験はありませんか。この物体を浮かび上がらせる力が浮力です。
物体を沈めるとき、物体の分だけ水は押しのけられてしまいます。押しのけられた水はもとどおりになろうと押し返します。つまり浮力とはこの押し返す力であり、押しのけた水の重さと同じだけの力です。
水に浮くものと沈むものがあるのはどうして?
水に浮く物体と沈む物体の違いはどこで決まるのでしょうか。これは物体の1cm3あたりの重さで決まります。たとえば、1cm3あたり5gの物体があったとします。これを水に入れると押しのけられる水は1cm3、つまり1gの浮力がかかります。しかし物体の重さは5gなので浮力で押し上げることはできません。結果、物体は沈んでしまいます。
沈んだ物体の浮力について考えよう
水1cm3を1gとします。その場合、50cm3の物体を沈めると50gの水を押しのけたことになりますから、浮力は50gです。
浮いている物体の浮力について考えよう
たとえば50gの物体が浮いているとします。物体が水面に浮くときは物体の重さと浮力が等しいときです。要するに、物体の重さで水を押した分だけ押し返されていて沈みません。50gの物体が浮かんでいるということは押しのけた水の重さも50gですから、物体のうち50cm3だけ沈んでいて残りが水面に出ている計算になります。
計算問題で出やすい立方体の浮力
浮力を表す式は下記となります。
立方体や円柱といった体積を求めやすい形状の物体を沈める問題は多いです。直方体を沈めるところを想像してみましょう。底面積が30cm2の物体を高さ5cm分沈めたとします。当然、沈んでいる部分の体積は30cm2 × 5cm = 150cm3となりますね。水1cm3あたりの重さは1gです。つまり150gの浮力がかかっている計算になります。
水溶液が解けない。覚える知識が多くてもひとつずつ
水溶液の問題は覚える知識が多く、更に計算問題も多いため注意が必要です。
水溶液とはなにか
水溶液について子供に説明を求めると「なにかが溶けている水」と答えを返されることが多いです。しかしその説明は十分ではありません。水溶液は溶け残しがなく透明です。均一に混ざっています。置いておいても、粒が水面に浮いてくるような事態にはなりません。その辺りもあわせて説明できるようにしておきましょう。
水溶液の濃度の式
水溶液の濃度はどう求めればよいのでしょうか。
水溶液の濃度を表す式は下記となります。
どういうことかといえば、水溶液100g中に砂糖が25g解けていたとします。そうすると、(25 ÷ 100)× 100となり、答えは25%です。
水溶液同士を混ぜる問題
水溶液同士を混ぜ合わせる問題もよく出てきます。
たとえば、下記の様な内容です。
水溶液の問題を解く際には、混ぜ合わせる過程ごとにビーカーの絵を描き、その横になにが何g溶けているか、水溶液の濃度はいくつかといった情報を書き込むことをおすすめします。
たとえば、この場合は100gで5%、つまり5gの食塩が溶けている食塩水の絵と、200gで8%、つまり16gの食塩が溶けている食塩水の絵をそれぞれ描き、混ぜ合わせたあとの300gで5gと16gであわせて21gの食塩が溶けている食塩水の絵を描きます。混ぜる前と混ぜた後でどう条件が変化したのか、ひと目でわかるよう図示しておくとよいでしょう。
最終的には、300gの中に21gの食塩が溶けていると判明したわけですから計算をすると、
つまり7%の食塩水が300gできたとわかります。
問題によって、水溶液をさらに混ぜ合わせたり、一部取り出したりしてより複雑な計算を求められますが、ビーカーの絵をその都度書き、いま水溶液は何gか、溶けているモノは何gか濃度は何%かを書きだしていけば解きやすいです。
水溶液の濃度を面積図で解く?
中学受験における水溶液の問題は面積図を使って解く機会も多いです。面積図を使って解く際は横を水溶液の重さ、縦を水溶液の濃度として考えると解きやすいです。
例題を解いてみましょう。
この場合、横が食塩水の重さ、縦が濃度の面積図を描きます。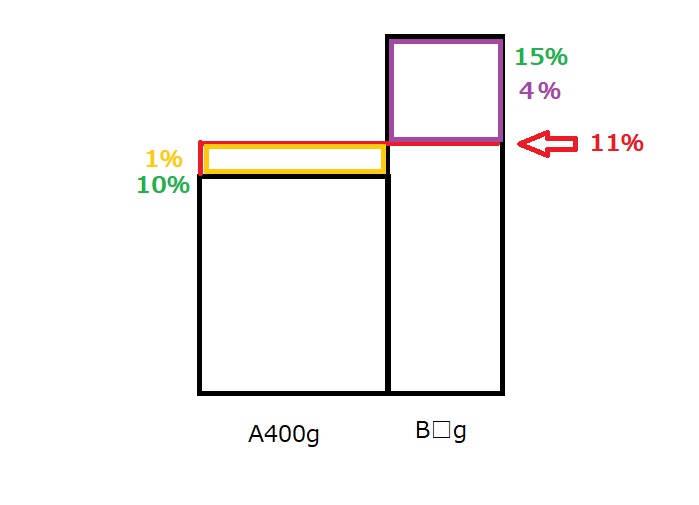 まず、面積図の横は(A)400gと(B)□gです。
まず、面積図の横は(A)400gと(B)□gです。
縦は(A)10%と(B)15%で、混ぜると11%になるため、混ぜる前の(A)(B)それぞれの濃度と混ぜ終えた後の濃度とを比べると(A)は1%、(B)は4%の差です。
そこまで面積図に書き込んだらあとは横が400gで高さが1%の部分と、(B)の横が□gで高さが4%の部分の面積が等しくなるものとして計算します。つまり高さが1%と4%で1:4なのですから横は4:1になるわけです。
したがって、(A)400gに対し(B)は100gになります。
受験本番が迫ってきたらどう勉強する?

受験本番直前になったら、どう仕上げていくのがよいのでしょうか。
優先順位を改めて決めよう
出題範囲を満遍なく勉強できればよいですが、いくつかの単元の仕上げが間に合わないケースもよくあります。一月になったら、どの単元が弱いのかを洗い出して、改めて優先順位を整理し直しましょう。この作業は家庭だけで行わないようにしてください。必ず塾講師や家庭教師の先生のアドバイスを受けましょう。
受験本番直前で勉強が間に合わなくなってくると、受験本番に志望校でなにが出題されるのか予想して、ピンポイントに学習していくやり方をとらざるを得ません。できるだけベテランの先生に予想してもらってください。
分野ごとのポイントを押さえた勉強を
理科の勉強は分野ごとに重視するべき箇所が違います。
生物の勉強の仕方
生物は知識量が問われます。過去問をやったときに、生物で点がとれていない子供は理科にかける勉強時間が少ないタイプが多いです。暗記はぎりぎりでも挽回がきくと思って油断していると、社会ともども追い込みが間に合わない事態に陥りかねません。少しずつ消化して、最後は苦手なところだけやり直せるようにしておきましょう。
地学の勉強の仕方
地学では、実際に星空を見上げながら覚えると暗記もスムーズです。天気の良い日に試せば、二等星ぐらいまでならある程度都会でも把握できます。四季の代表的な天体については暗記力が問われますが、問題によっては計算力も問われます。天体の動きはその代表例です。理屈を理解したら、問題数をこなして確実に解けるレベルに仕上げましょう。
化学の勉強の仕方
化学は実験道具の名称や正しい使い方、手順を覚えることが大切です。その上で、公式や面積図を使って答えを求めましょう。面積図はひとりで描けるようになるまで時間がかかる子供が多いです。何度も挑戦して仕上げていきましょう。
物理の勉強の仕方
苦手な子供が非常に多い物理では、問題をやり込む必要があります。数をこなし、基礎だけではなく応用まで対応できるようにしましょう。いろんな角度から切り込んだ問題が出題されるので、ひとつの単元で数問解けたからといってわかった気にならない姿勢が重要です。
苦手な単元こそ積極的に勉強を

理科の過去問をやり込んでいくと、自分の得意不得意がはっきり見えてきます。しかし、苦手な単元を仕上げないまま問題を放置する子供は少なくありません。
本来、苦手な単元こそ積極的に勉強する必要があります。難しくてなかなか理解できそうにないと思ったら塾の先生や家庭教師の先生に質問に行き、解説してもらってから解くようにしましょう。受験本番が近づけば近づくほど、タイムロスを減らし、きっちり実力を定着化させる必要があります。先生に解説してもらえれば、「ああでもないこうでもない」と悩む時間は削減できるはずです。
ただし、自分で考える時間が減った分、復習に注力する必要があります。解説してもらった問題の内容を理解し、自力で解けるように問題をやり込むことに時間を割きましょう。
この記事で紹介した、電流・浮力・水溶液は子供たちが苦手とする単元の代表例です。ぜひ記事で紹介したような基本事項を理解した上で、多くの問題に挑むことをおすすめします。














